Was riesige Schwarze Löcher mit dem Urknall zu tun haben
Schwarze Löcher gibt es in allen möglichen Größen. Es gibt sie – vermutlich – in ganz klein, quasi in “S” oder “M”, hier steht der Nachweis noch aus. Es gibt Schwarze Löcher mit der Masse einiger Sterne, die als Überbleibsel von Supernovae entstehen. Dieses “L” ist wohl die Standardgröße. Dann gibt es die XL-Variante, die sich im Zentrum der meisten Galaxien findet. Und schließlich existiert auch noch die XXL-Version, die Astronomen in 13 Milliarden Lichtjahren Entfernung gefunden haben – die also kurz nach dem Urknall (in astronomischen Zeiträumen gesehen) geboren worden sein muss.
Bei letzterer ist jedoch bisher nicht klar, welcher Prozess sie ins Leben gerufen haben könnte. Handelt es sich um Nachkommen der allersten Sterne? Oder hat sich an diesen Stellen die dichte Ur-Wolke direkt zu einem Schwarzen Loch verwirbelt und zusammengeballt? Beide Vorstellungen haben ihre jeweils eigenen Probleme. In Science stellen die japanischen Forscher Shingo Hirano und Naoki Yoshida jetzt einen Geburtshelfer vor, der zumindest in zeitlicher Nähe aktiv war: den Urknall selbst.
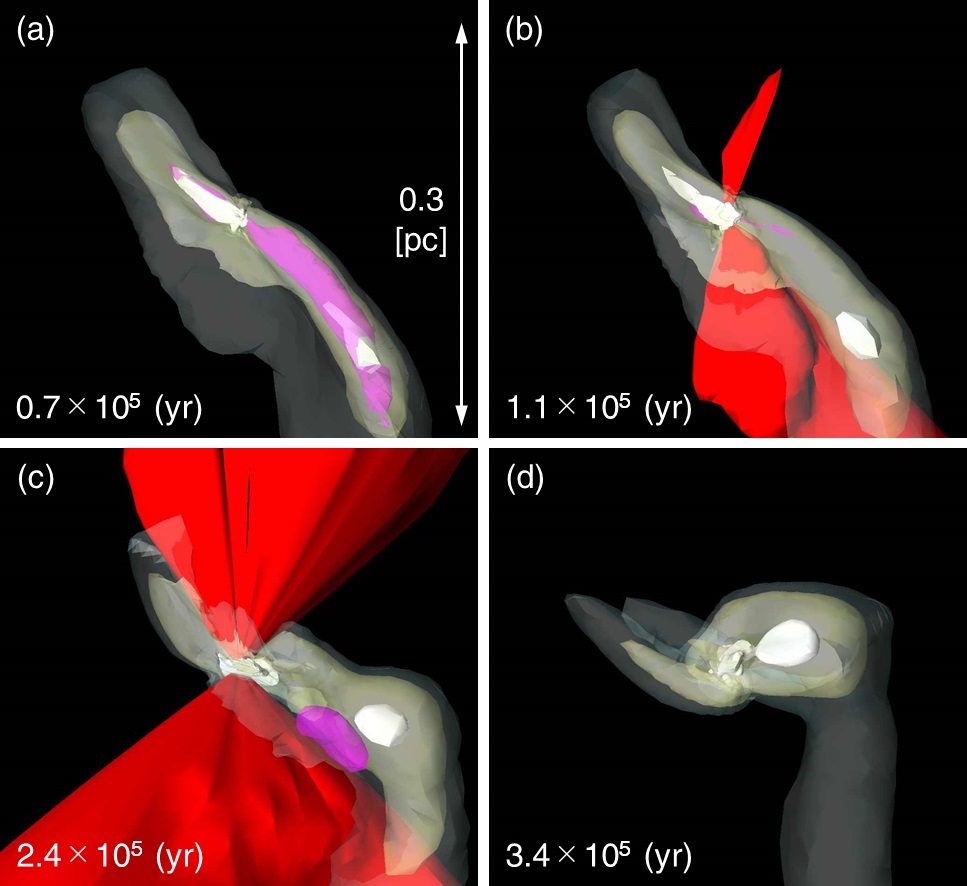
Die Forscher haben im Supercomputer die Verhältnisse kurz nach dem Big Bang simuliert. Als das Universum erst 100 Millionen Jahre alt war, muss sich ein dichter Klumpen Dunkler Materie herausgebildet haben. Dieser wurde dann von noch vom Urknall übrig gebliebenen überschallschnellen Gasströmen getroffen, so dass sich eine dichte, turbulente Gaswolke bildete. In ihr entstand schnell ein Protostern, und da die Gaswolke genügend Futter enthielt, wuchs er auf riesige Ausmaße.
Das konnte nicht allzu lange gut gehen: Als der Riesenstern 34.000 Sonnenmassen schwer war, kollabierte er unter seiner eigenen Gravitation und hinterließ ein superschweres Schwarzes Loch. Dass es sich dabei um mehr als ein Theorie handeln könnte, zeigt der Vergleich mit der Wirklichkeit: Aus der Simulation ergibt sich, dass so etwa ein Schwarzes Loch in einem Volumen von 3 x 3 x 3 Milliarden Lichtjahren entstanden sein muss – was ziemlich nah an der tatsächlich nachgewiesenen Zahl liegt.
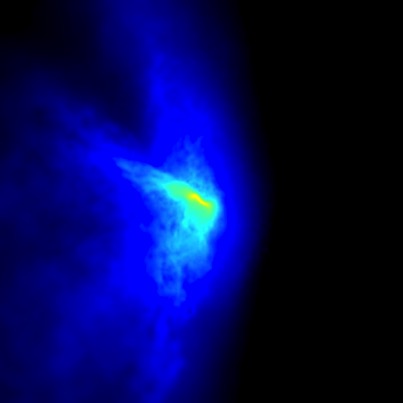
(Bild: Shingo Hirano)